ケィオスの道具としての数学

科学技術への入り口として，数理を解説したいと思います．

【複素関数の積分】（１）複素積分で覚えておきたいポイント

複素関数論

複素積分について勉強したでしょうか．私は数学者ではありませんが，昔，ある大学で，線形代数とか，複素関数論とか，数学の基礎科目の講義を一通り担当していました．毎週6～7コマ担当なので，結構疲れて，肩が痛かったです．その当時は，お前の仕事は講義と大学の雑用で，お前の研究成果なんて誰も評価しないぞ，というような環境でしたが，研究は好きだったので細々と続けていました．ということで，昔作成した図を使って，今回は複素積分で印象に残しておいてほしいポイントをまとめます．

点Pから点Qまでの線積分

複素積分

　関数 $f(z) = u(x, y) + v(x, y)\, i$ と曲線 $C: z = z(t) = x(t) + i y(t)$ $(a\, \le \, t \,\le \, b)$ を考える．このとき， $f(z)$ の曲線 $C$ に沿っての複素積分は，

$\begin{eqnarray} \int_C \! f(z) \, dz &=& \int_C \! \left\{u(x,y) + v(x,y)\, i \right\}(dx + dy \, i) \nonumber \\ &=& \int_C \! (u \, dx - v \, dy) + i \int_C \! (v \, dx + u \, dy) \nonumber \end{eqnarray}$

です． $u(x, y)$ とか $v(x, y)$ の積分は上の図でイメージしてください．要は，線積分の寄せ集めです．

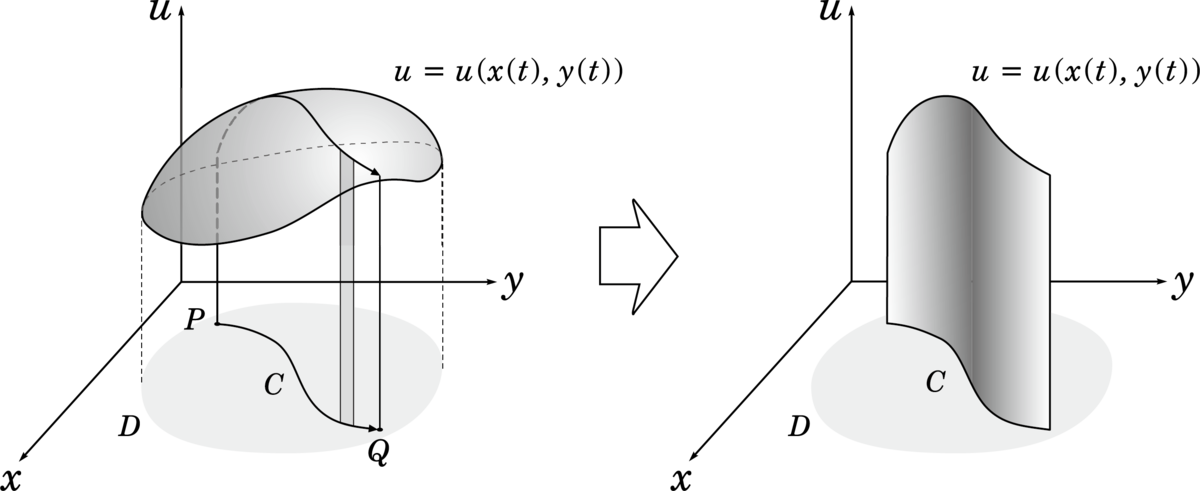
不定 積分が存在するときの積分

　ここから，ラフに説明していきます．「不定積分が存在するとき」というのは，積分したい関数 $f(z)$ に，

　 $\displaystyle \frac{d F(z)}{dz} = f(z)$

となる相手 $F(z)$ がいるときです．高校で習う積分の公式があるようなときです．積分経路を含む領域で正則だったら，その領域で，積分は積分経路によらず，端の点の値だけできまります．正則というのは，その点で微分できると言うことです．コーシー・リーマンの方程式が何かも知っておいてください．

複素平面上の領域 $D$ 内に曲線 $C$ をとり，その始点と終点をそれぞれ $p$ , $q$ とする (下図)．このとき， $D$ 内で正則な関数 $f(z)$ の不定積分 $F(z)$ が存在すれば，

　 $\displaystyle \int_C \! f(z) \, dz = F(q) - F(p)$

不定積分が存在する場合は，実数の積分のように，積分の公式を使って出発点pと終点qの値を代入すればいいんです．

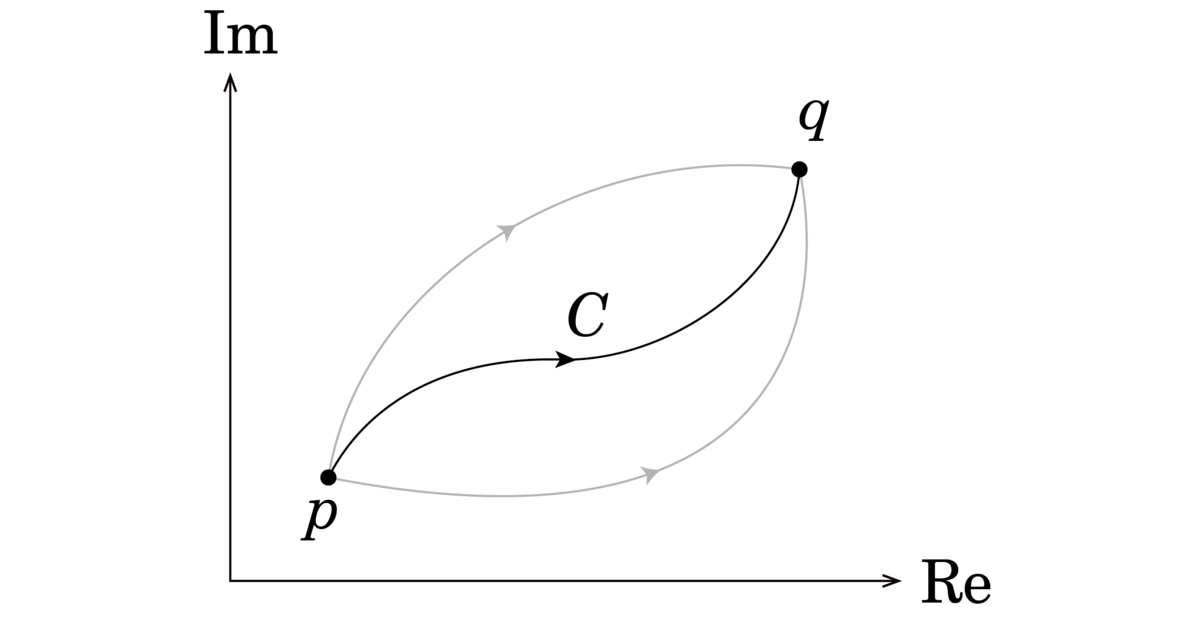
コーシー (Cauchy)の積分定理

　ここから単一閉曲線での積分です．「単一」は自分に交わらない，「閉曲線」はぐるぐる何周でも回れるようにつながっているということです (下図)．例えば，円です．いつも左周りが正の向きです．

単一閉曲線とそうじゃないやつ

　まずは，計算せずに答えを0と書ける，お得なパターンです．

関数 $f(z)$ は，単一閉曲線 $C$ とその内部を含む領域で正則であるとする (下図)．このとき，

　 $\displaystyle \oint_C \! f(z) \, dz = 0$

単一閉曲線の積分経路．内部に穴がある (分母が発散する)かどうかを確認してください．穴がなければ，コーシーの積分定理が使えます．

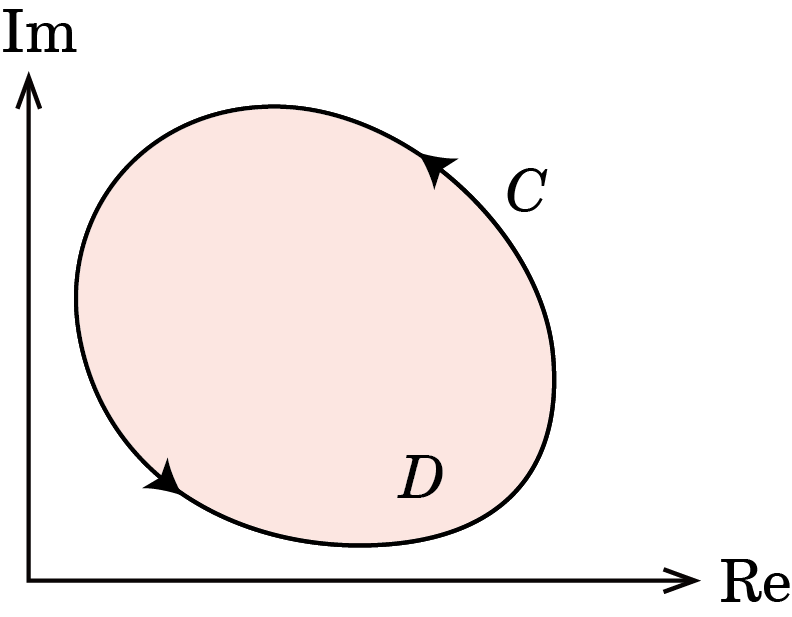
　以下のような問題に出会ったら，答えは0だと，3秒以内に気づいてください．

問題　 $C$ を任意の単一閉曲線とするとき，次の積分を求めよ．

　 $\displaystyle (1) \ \oint_C \! z^3 \, dz, \qquad (2) \ \oint_C \! e^{iz} \, dz \qquad (3) \ \oint_C \! \sin z \, dx$

周回積分と積分路

　周回積分の積分経路を変えられるという話です．証明は，下の図のように経路を切ってみるという，気づければ意外と簡単なやつです．

経路を切ってコーシーの積分定理を使うと証明できる

領域 $D$ で $f(z)$ は正則関数であるとする． $D$ 内に2つの単一閉曲線 $C_1$ , $C_2$ があり， $C_2$ は $C_1$ の内部にあるとする．さらに， $C_1$ , $C_2$ で囲まれた領域は，領域 $D$ に含まれているとする．このとき，

　 $\displaystyle \oint_{C_1} \! f(z) \, dz = \oint_{C_2} \! f(z) \, dz$

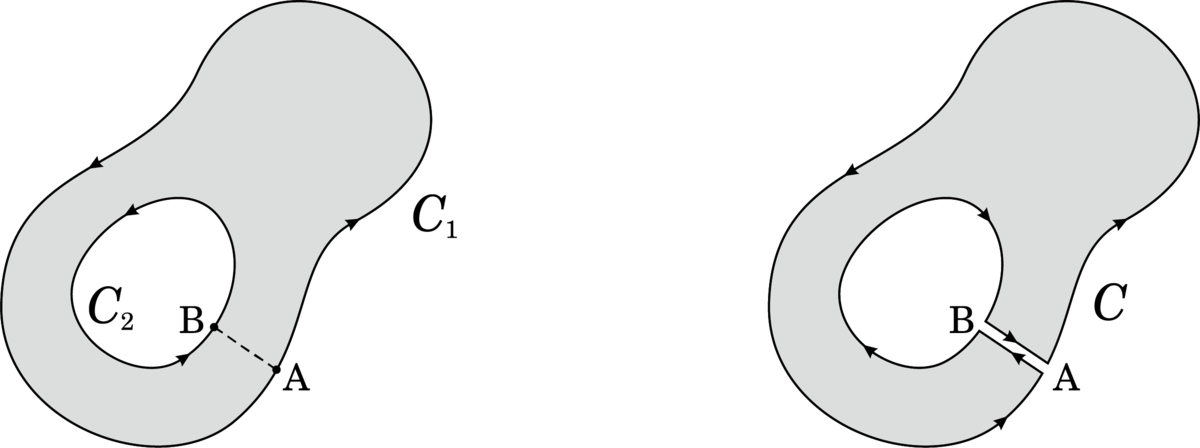
コーシーの積分表示 (コーシーの積分定理)

　被積分関数に，微分できない穴 (発散する点)があるときの積分です．分母がゼロになる点は，穴とか，トゲとか，針とか，そういうイメージをもってください．ここで穴と呼んでいる点の，専門用語は「特異点」です．上で説明した性質を使って，積分経路を，穴へ縮めていけば証明できます．

$f(z)$ は領域 $D$ で正則であるとする． $D$ 内に単一閉曲線 $C$ があり， $C$ の内部は領域 $D$ に含まれているとする. 点 $a$ が $C$ の内部にあれば (下図)，

　 $\displaystyle f(a) = \frac{1}{2 \pi i} \oint_C \frac{f(z)}{z-a} \, dz$

閉曲線Cの中に穴 (トゲ)があるとき．

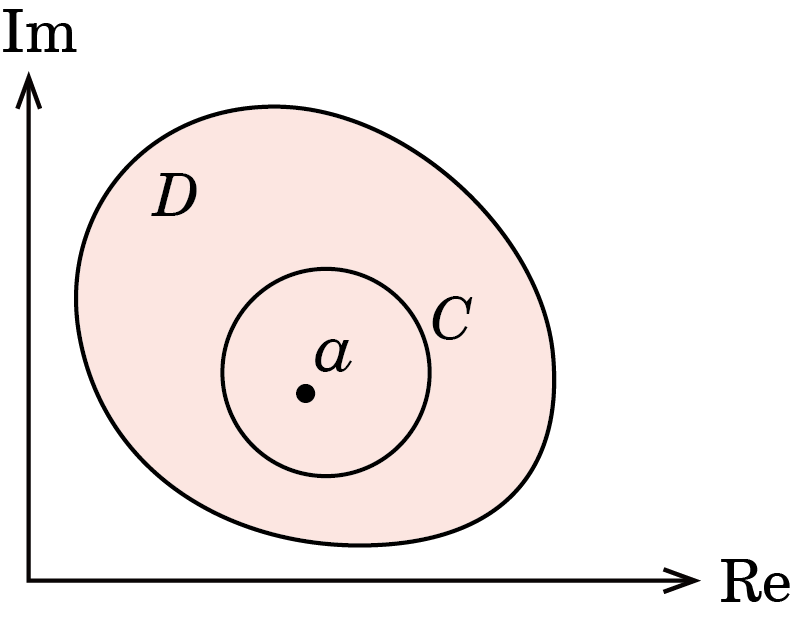
　積分の公式的に使いたいときは，以下の印象をもっておいてください．

積分経路の中に発散する穴 $a$ (分母が0になる点)が空いていれば，積分は分子の部分に穴の値を代入するだけで求まっちゃう．

　 $\displaystyle \oint_C \frac{f(z)}{z-a} \, dz = 2 \pi i f(a)$

　以下のような問題に出会ったら，10秒以内に答えを書いてください．

問題　 $C$ を原点を中心とする半径2の円とするとき，次の積分を求めよ．

　 $\displaystyle (1) \ \oint_C \frac{1}{z-1} \, dz, \qquad (2) \ \oint_C \frac{z^2}{z-i} \, dz \qquad (3) \ \oint_C \frac{e^z}{z-10000} \, dz$

グルサー (Goursat)の公式

　コーシーの積分表示で，穴が $n$ 乗のパターンです．コーシーの積分表示の両辺を微分すれば導けます．

$f(z)$ は領域 $D$ で正則であるとする．さらに， $D$ 内で $f(z)$ は何回でも微分可能とする．このとき， $f(z)$ の $n$ 階導関数

　 $\displaystyle f^{(n)}(z) = \frac{d^n f(z)}{dz^n}$

は

　 $\displaystyle f^{(n)}(z) = \frac{n!}{2 \pi i} \oint_C \frac{f(\zeta)}{(\zeta-z)^{n+1}} \, d \zeta$

　これも公式的に使いたいときは，以下の印象をもっておいてください．

積分経路の中に発散する穴 $a$ (分母が0になる点)が空いていて，それが $n$ 乗でより深くなっていれば，

　 $\displaystyle \oint_C \frac{f(z)}{(z-a)^{n}} \, d z = \frac{2 \pi i}{(n-1)!} f^{(n-1)}(a)$

　ここまでの複素積分を使いこなせれば，留数定理が成り立つことは，当然と感じられると思います．留数定理は次回です．